含有非局部項的半線性橢圓方程

研究介紹
最近幾年來我的研究主要是利用變分法來探討含有非局部(nonlocal)項的半線性橢圓方程之相關兩類問題，主要成果如下：
(I) Kirchhoff 型式之半線性橢圓方程：

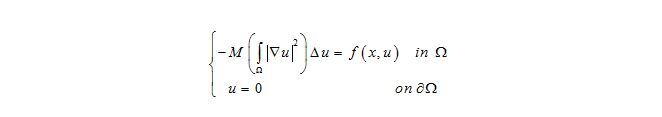
Kirchhoff型式之半線性橢圓方程:

其中 Ω為 RN 空間上的定義域，M(s)= as+b且a,b, λ>0, 且  f( x ,u) 為非線性項。此方程為描述下列Kirchhoff 型半線性雙曲方程的基態行為：

Kirchhoff型半線性雙曲方程的基態行為

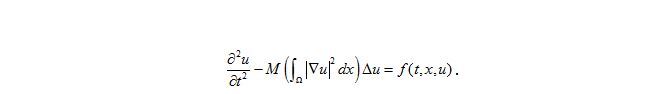
這類型的雙曲方程為出現在物理中的非線性共振理論中，而其有解性也在數學中被討論。這類型的方程式，首次是由Kirchhoff 在1883 年所提出，主要是描述彈性弦的橫波。特別是像這樣的模型代表著會改變弦長的震盪，其中u代表位移、  f( t, x, u ) 代表外力而b代表起始張力，而a是與弦本身內在的性質有關(例如：Young's modulus)上述的問題常與非局部性有關聯，這是因為它在於整個定義域是可積的。而到目前為止在大量文獻紀錄中許多的研究結果，大都利用非線性項在適當的假設下來證明方程式(E)的正解之存在性或多重性。而對於該方程，我們首度發展出許多數學上的新理論與工具，從而獲得重大突破。

(II) 非線性Schrödinger-Poisson 系統：

非線性Schrödinger-Poisson系統

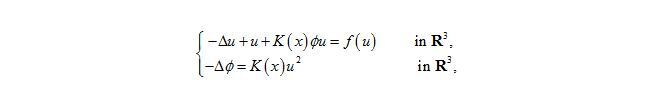
其中K為非負函數(nonnegative function)，而非線性項 f：R→ 為 Carathéodory 函數。此類問題為研究非線性Schrödinger 場與電磁場(electromagnetic fields) (𝐸, 𝐻) 之間的交互作用下時駐波解的定性行為。而我們針對非負函數K 或非線性項f(u)在不同的假設下進行研究，而Schrödinger-Poisson 系統在適當的偶合之下會出現正解的對稱破壞(symmetry breaking)，這問題已經將近20 年一直是全世界相關領域專家想要解決的問題。目前我們已經有相當大的進展了，我們目前已經證明了當非線性項 f (u)為 3-sublinearity 時，非線性 Schrödinger-Poisson 系統會有非徑向對稱基態解的存在以及多解性。此外，我們也發展了許多新的數學理論來攻克了許多問題，例如：多解性與高能解的存在性。

 

 

參考文獻

  1. J. Zhang, J. Sun, Tsung-fang Wu* (2021) Positive bound state solutions for non-autonomous Schrödinger-Poisson systems with 2<p<4, Zeitschrift fuer Angewandte Mathematik und Physik,72:162. (SCI)
  2.  Tsung-fang Wu* (2021) Existence and symmetry breaking of ground state solutions for Schrödinger-Poisson Systems, Calculus of Variations and Partial Differential Equations 60:59. (SCI)
  3. J. Sun, K. H. Wang and Tsung-fang Wu* (2021) On indefinite Kirchhoff-type equations under the combined effect of linear and superlinear terms, Journal of Mathematical Physics 62, 031505. (SCI)
  4. J. Sun and Tsung-fang Wu* (2021) The number of nodal solutions for the Schrödinger-Poisson system under the effect of the weight function, Discrete and Continuous Dynamical Systems-Series A 41, 3651-3682. (SCI)
  5.  J. Sun* and Tsung-fang Wu (2021) On Schrödinger-Poisson systems involving concave-convex nonlinearities via a novel constraint approach, Communications in Contemporary Mathematics Vol. 23, No. 6, 2050048 (25 pages). (SCI)
  6. J. Sun and Tsung-fang Wu* (2020) On Schrödinger-Poisson systems under the effect of steep potential well (2<p<4), Journal of Mathematical Physics 61, 071506. (SCI)
  7.  H. Zhang, T. Li, Tsung-fang Wu* (2020) On the solvability of an indefinite nonlinear Kirchhoff equation via associated eigenvalue problems, Journal of Differential Equations 269, 2853-2895.(SCI)
  8.  J. Sun and Tsung-fang Wu* (2020) Bound state nodal solutions for the non-autonomous Schrödinger-Poisson system in 3 , Journal of Differential Equations 268, 7121-7163. (SCI)
  9.  J. Sun*, Y. H. Cheng, Tsung-fang Wu and Z. Feng (2019) On positive solutions of a superlinear Kirchhoff type equation in R^N (N>=4), Communications in Nonlinear Science and Numerical Simulation 71, 141-160. (SCI)
  10. J. Sun*, Tsung-fang Wu, Zhaosheng Feng (2019) Two Positive Solutions to Non-autonomous Schrodinger-Poisson Systems, Nonlinearity 32, 4002. (SCI)
     

作者：吳宗芳 教授
單位：國立高雄大學應用數學系