研究介紹

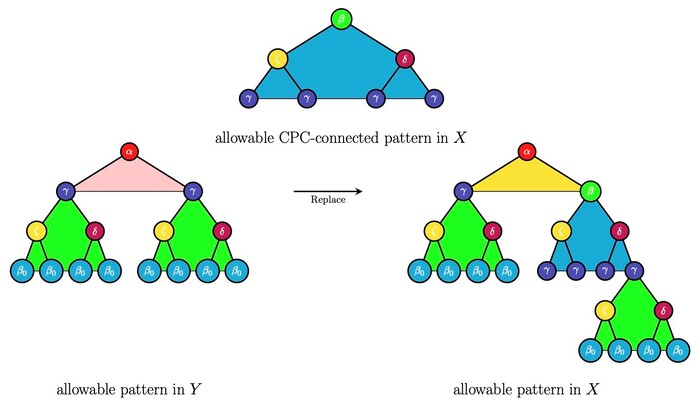
        符號學在各行各業有著廣泛的應用，例如資訊傳送、資料壓縮，以及加密、解密等等；除此之外，符號學也大量用於探討電磁效應或相變等物理現象。傳統的研究以一維及二維網格為主流，更高維度的網格甚至不規則的空間結構的討論相對缺乏，近幾年來，針對樹狀結構等非網格空間的符號學研究如雨後春筍般蓬勃發展，除了單純的學術研究以外，一方面也是發現這些研究方向和物種繁衍等問題有著密切關連。

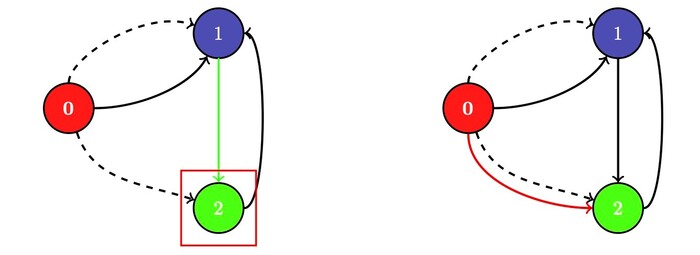
        我們這幾年來，投注了不少心力在樹狀結構空間中的符號學研究，主要集中在複雜度與隨機性兩大方向。複雜度除了告訴我們系統所蘊含(或說儲存)的資訊量以外，其實也和不可預測性有關，而所謂的不可預測性，簡單來說就是某種程度的隨機性。由於複雜度這樣的統計量無法完整呈現隨機性，我們進一步透過拓樸手法來區別不同程度的隨機性，更重要的是，藉由圖論的技巧，我們發展出一套演算法協助判斷給定系統的隨機性。同時，我們證明了在具備一定程度的隨機性之後，渾沌現象也隨之產生。

主要成果 (參考文獻)

1. J.-C. Ban and C.-H. Chang*, Complexity of neural networks on Fibonacci-Cayley tree, J. Algebra, Combinatorics, Discrete Structures and Applications 6, 105-122, 2019.

2. J.-C. Ban, C.-H. Chang*, N.-Z. Huang and Y.-L. Wu, Decidability of irreducible tree shifts of finite type, J. Stat. Phys. 177, 1043-1062, 2019.

3. J.-C. Ban and C.-H. Chang*, Tree-Shifts: Irreducibility, mixing, and the chaos of tree-shifts, Trans. Amer. Math. Soc. 369, 8389-8407, 2017.

4. J.-C. Ban and C.-H. Chang*, Tree-Shifts: The entropy of tree-shifts of finite type, Nonlinearity 30, 2785-2804, 2017.

5. J.-C. Ban and C.-H. Chang*, Mixing properties of tree-shifts, J. Math. Phys. 58, 112702, 2017.

作者：張志鴻       教授

單位：國立高雄大學應用數學系